Рассмотрим реализацию выборки на одном элементарном исходе ![]() —
набор чисел
—
набор чисел ![]() ,
, ![]() ,
, ![]() .
На подходящем
вероятностном пространстве введем случайную величину
.
На подходящем
вероятностном пространстве введем случайную величину ![]() ,
принимающую значения
,
принимающую значения ![]() ,
, ![]() ,
, ![]() с вероятностями по
с вероятностями по ![]() (если какие-то из значений совпали,
сложим вероятности соответствующее число раз). Таблица распределения
вероятностей и функция распределения случайной величины
(если какие-то из значений совпали,
сложим вероятности соответствующее число раз). Таблица распределения
вероятностей и функция распределения случайной величины ![]() выглядят так:
выглядят так:
|
|
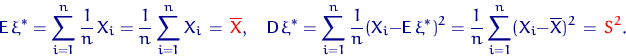
Точно так же вычислим и момент порядка ![]()
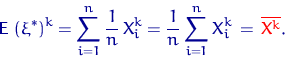
В общем случае обозначим через ![]() величину
величину
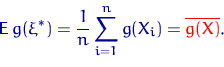
Если при построении всех введенных нами характеристик считать выборку
![]() ,
, ![]() ,
, ![]() набором случайных величин,
то и сами эти характеристики —
набором случайных величин,
то и сами эти характеристики — ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() — станут величинами случайными. Эти характеристики
выборочного распределения используют для оценки (приближения) соответствующих
неизвестных характеристик истинного распределения.
— станут величинами случайными. Эти характеристики
выборочного распределения используют для оценки (приближения) соответствующих
неизвестных характеристик истинного распределения.
Причина использования характеристик распределения
![]() для оценки характеристик истинного распределения
для оценки характеристик истинного распределения ![]() (или
(или ![]() )
— в близости этих распределений при больших
)
— в близости этих распределений при больших ![]() .
.
Рассмотрим, для примера,
![]() подбрасываний правильного кубика. Пусть
подбрасываний правильного кубика. Пусть ![]() —
количество очков, выпавших при
—
количество очков, выпавших при ![]() -м броске,
-м броске, ![]() .
Предположим, что единица в выборке встретится
.
Предположим, что единица в выборке встретится ![]() раз, двойка —
раз, двойка — ![]() раз
и т.д.
Тогда случайная величина
раз
и т.д.
Тогда случайная величина ![]() будет принимать значения 1,
будет принимать значения 1, ![]() , 6
с вероятностями
, 6
с вероятностями ![]() ,
, ![]() ,
, ![]() соответственно.
Но эти пропорции с ростом
соответственно.
Но эти пропорции с ростом ![]() приближаются к
приближаются к ![]() согласно закону больших чисел. То есть распределение
величины
согласно закону больших чисел. То есть распределение
величины ![]() в некотором смысле сближается с истинным распределением
числа очков, выпадающих при подбрасывании правильного кубика.
в некотором смысле сближается с истинным распределением
числа очков, выпадающих при подбрасывании правильного кубика.
Мы не станем уточнять, что имеется в виду под близостью выборочного и истинного распределений. В следующих параграфах мы подробнее познакомимся с каждой из введенных выше характеристик и исследуем ее свойства, в том числе ее поведение с ростом объема выборки.
N.I.Chernova