Критерий ![]() (K.Pearson, 1900) основывается на группированных данных.
Область значений предполагаемого распределения
(K.Pearson, 1900) основывается на группированных данных.
Область значений предполагаемого распределения ![]() делят на некоторое число интервалов.
После чего строят функцию отклонения
делят на некоторое число интервалов.
После чего строят функцию отклонения ![]() по разностям
теоретических вероятностей попадания в интервалы
группировки и эмпирических частот.
по разностям
теоретических вероятностей попадания в интервалы
группировки и эмпирических частот.
Имеется выборка ![]() из распределения
из распределения ![]() . Проверяется простая гипотеза
. Проверяется простая гипотеза ![]() против сложной альтернативы
против сложной альтернативы ![]() .
.
Пусть, как в параграфе 1.6,
![]() ,
, ![]() ,
, ![]() — интервалы группировки в области
значений случайной величины с распределением
— интервалы группировки в области
значений случайной величины с распределением ![]() .
Обозначим для
.
Обозначим для ![]() через
через ![]() число элементов выборки,
попавших в интервал
число элементов выборки,
попавших в интервал ![]()
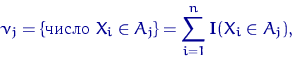
и через ![]() — теоретическую вероятность
— теоретическую вероятность ![]() попадания в интервал
попадания в интервал ![]() случайной величины с распределением
случайной величины с распределением
![]() . С необходимостью,
. С необходимостью, ![]() . Как правило,
длины интервалов выбирают так, чтобы
. Как правило,
длины интервалов выбирают так, чтобы ![]() .
.
Пусть
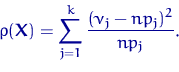 | (23) |
Свойство K1(б) выполнено далеко не для всех альтернатив.
Если распределение выборки ![]() имеет такие же,
как у
имеет такие же,
как у ![]() , вероятности
, вероятности ![]() попадания в каждый из интервалов
попадания в каждый из интервалов
![]() , то по данной функции
, то по данной функции ![]() эти распределения различить невозможно.
эти распределения различить невозможно.
Поэтому на самом деле критерий, который мы построим по функции ![]() из
(23),
решает совсем иную задачу. А именно, пусть задан набор вероятностей
из
(23),
решает совсем иную задачу. А именно, пусть задан набор вероятностей
![]() такой, что
такой, что ![]() . Критерий
. Критерий ![]() предназначен
для проверки сложной гипотезы
предназначен
для проверки сложной гипотезы
![]()
против сложной альтернативы ![]() , т.е.
, т.е.
![]()
Покажем, что ![]() удовлетворяет условию
K1(a).
удовлетворяет условию
K1(a).
Если верна гипотеза ![]() ,
то при фиксированном
,
то при фиксированном ![]() и при
и при ![]()
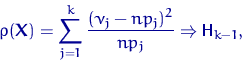
где, напомним, ![]() есть
есть ![]() -распределение с
-распределение с ![]() степенью свободы.
степенью свободы.
|
Стоит остановиться и задать себе вопрос. Величина Причина кроется, конечно, в зависимости слагаемых: |
Докажем теорему Пирсона при ![]() .
.
В этом случае ![]() ,
, ![]() . Посмотрим на
. Посмотрим на ![]() и
вспомним ЦПТ:
и
вспомним ЦПТ:
![]()
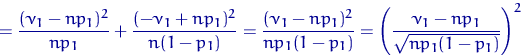 .
.
Но величина ![]() есть сумма
есть сумма ![]() независимых случайных величин
с распределением Бернулли
независимых случайных величин
с распределением Бернулли ![]() , и по ЦПТ
, и по ЦПТ
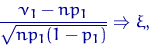
где ![]() имеет стандартное нормальное распределение. Поэтому
имеет стандартное нормальное распределение. Поэтому
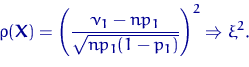
Величина ![]() имеет
имеет ![]() -распределение
-распределение ![]() с одной степенью свободы.
с одной степенью свободы.
Q.D.E.
| Для экономистов, только приступающих к знакомству с многомерным нормальным распределением, матрицами ковариаций и всевозможными квадратичными формами, составленными из (асимптотически) нормальных слагаемых, исключительно полезно познакомиться с доказательством теоремы Пирсона в общем случае. Параграф 1 приложения, который познакомит читателя с многомерным нормальным распределением, стоит напечатать и повесить в изголовье кровати до окончания курса эконометрики. |
Функция ![]() удовлетворяет условию
K1(б). Действительно,
удовлетворяет условию
K1(б). Действительно,
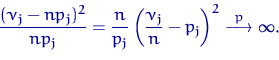
Осталось построить критерий в соответствии с K2.
Пусть случайная величина ![]() имеет распределение
имеет распределение
![]() . По таблице распределения
. По таблице распределения ![]() найдем
найдем ![]() равное квантили
уровня
равное квантили
уровня ![]() этого распределения.
Тогда
этого распределения.
Тогда ![]() и
критерий согласия
и
критерий согласия ![]() выглядит как все критерии согласия:
выглядит как все критерии согласия:

На самом деле критерий ![]() применяют и для решения первоначальной
задачи о проверке гипотезы
применяют и для решения первоначальной
задачи о проверке гипотезы ![]() .
Необходимо только помнить,
что этот критерий не состоятелен для альтернатив с теми же вероятностями
попадания в интервалы разбиения, что и у
.
Необходимо только помнить,
что этот критерий не состоятелен для альтернатив с теми же вероятностями
попадания в интервалы разбиения, что и у ![]() . Поэтому берут большое
число интервалов разбиения — чем больше, тем лучше, чтобы «уменьшить»
число альтернатив, неразличимых с предполагаемым распределением.
. Поэтому берут большое
число интервалов разбиения — чем больше, тем лучше, чтобы «уменьшить»
число альтернатив, неразличимых с предполагаемым распределением.
Сходимость по распределению ![]() обеспечивается ЦПТ, поэтому разница допредельной и предельной вероятностей
имеет тот же порядок, что и погрешность нормального приближения
обеспечивается ЦПТ, поэтому разница допредельной и предельной вероятностей
имеет тот же порядок, что и погрешность нормального приближения

(см. неравенство Берри — Эссеена для погрешности в ЦПТ),
где ![]() — некоторая постоянная. Маленькие значения
— некоторая постоянная. Маленькие значения ![]() в знаменателе
приведут к тому, что распределение
в знаменателе
приведут к тому, что распределение ![]() будет существенно
отличаться от
будет существенно
отличаться от ![]() . Тогда и реальная вероятность
. Тогда и реальная вероятность ![]() —
точный размер полученного критерия — будет сильно
отличаться от
—
точный размер полученного критерия — будет сильно
отличаться от ![]() .
Поэтому для выборки объема
.
Поэтому для выборки объема ![]() число интервалов разбиения выбирают
так, чтобы обеспечить нужную точность при замене распределения
число интервалов разбиения выбирают
так, чтобы обеспечить нужную точность при замене распределения
![]() на
на ![]() .
.
Обычно требуют, чтобы
![]() были не менее
были не менее ![]() -
-![]() .
.
N.I.Chernova